Lattice Path Combinatorics

Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.

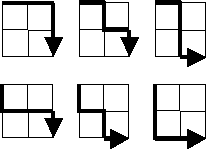
How many such routes are there through a 20×20 grid?

This question was posed on Project Euler, a site dedicated to problems that can be solved with mathematical and/or computational approaches (often both). The problem can be generalized to the following:

Start at the top-left intersection of an \(n\times n\) grid. By only moving to the right and down, how many unique routes to the bottom corner exist?

Finding a Solution

An initial intuition might be to break the problem into the simplest case: a 1x1 “grid”.

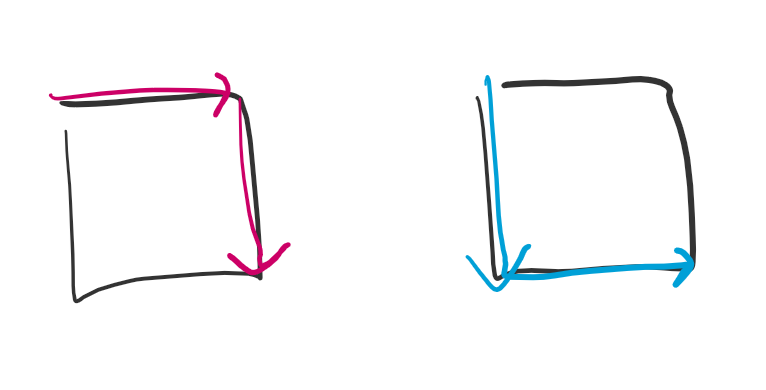
There are only 2 unique routes. The next logical step could be to see how many unique routes exist for a 3x3 grid in hopes that a common pattern would emerge to allow a generalization for an \(n\times n\) grid.

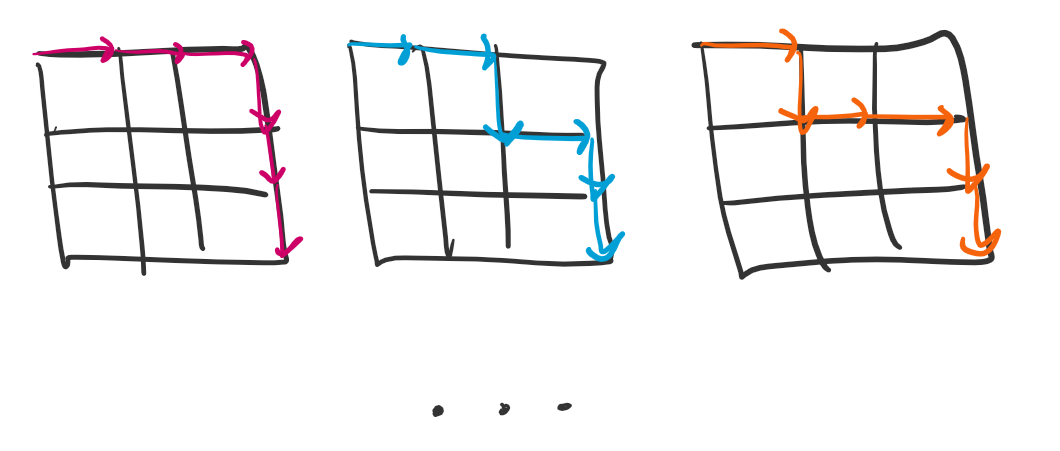
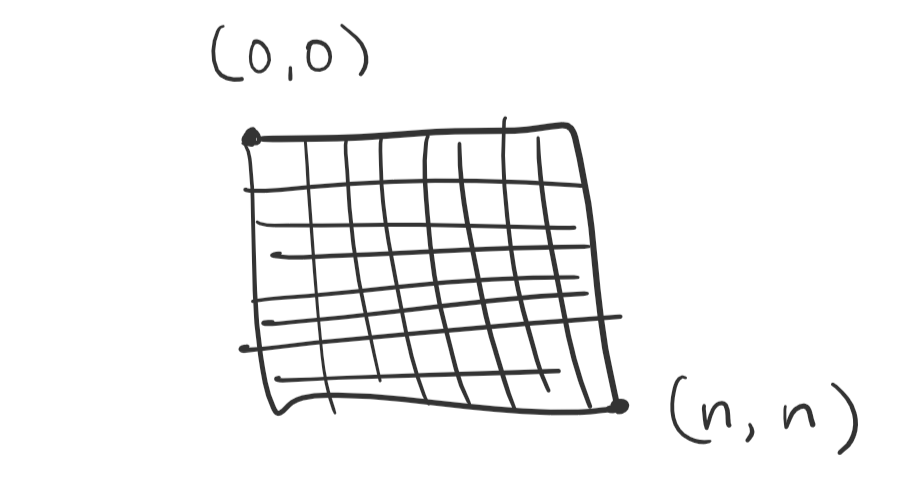
However, it becomes immediately apparent that the number of paths grows too quickly to count. But, drawing out the paths can reveal some useful facts. Notice that, because you can only move to the right and down, one step will always take you closer to the end. Therefore, the length of every route is the same. If we assign the coordinates \((0,0)\) to the top-left corner and the coordinates \((n,n)\) to the bottom-right corner, it becomes clear that the route must contain \(n\) rightward steps and \(n\) downward steps.

Let’s assign some notation to make this easier to think about. Let \(0\) denote a rightward step and \(1\) denote a downward step. A route then is a sequence containing \(2n\) bits, where $n$ of those bits are \(1\) and the other \(n\) are \(0\). Now the problem becomes one of combinatorics: How many different ways can you arrange a sequence of \(2n\) bits where half are set and the other other half are not?

This is a specific case of a common general combinatoric problem. First, how many permutations exist for a sequence of \(2n\) distinct elements? The first element can be placed in any of the \(2n\) places in the sequence. After that, the next element has \(2n-1\) different places it could go, the next has \(2n-2\) different places, etc. until the last one has only \(1\) place it could go. This gives \((2n)(2n-1)(2n-2)...(2)(1) = (2n)!\) permutations for a sequence of length \(2n\).

But, our bit sequence doesn’t have \(2n\) elements. It has \(2n\) places, but it only has \(n\) elements (\(1\)’s). So, we don’t fill the sequence until there are no places left; we stop when it is only half filled:

\[(2n)(2n-1)(2n-2)...(n+1)(n)\]

These are just the first \(n\) terms of \((2n)!\). We can get this by dividing \((2n)!\) by its last \(n\) terms so that they cancel out:

\[(2n)(2n-1)(2n-2)...(n+1)(n) = \frac{(2n)(2n-1)(2n-2)...(2)(1)}{(n)(n-1)...(2)(1)} = \frac{(2n)!}{n!}\]

We’re still not done though. This considers the number of unique sequence of length \(2n\) if all \(n\) elements are distinct. But, all the elements in our sequence are the same (\(1\)’s). There’s no difference between putting our 1st element in the 1st place and our 2nd element in the 2nd place versus putting our 1st element in the 2nd place and the 2nd element in the 1st. In other words, the order of our \(1\)’s doesn’t matter. So, we need to remove all the different ways the \(n\) elements could be permuted from our formula. Since there are \(n!\) different ways that \(n\) elements could be permuted,

\[\frac{(2n)!}{n!} \cdot \frac{1}{n!} = \frac{(2n)!}{(n!)^2}\]

there are \(\frac{(2n)!}{(n!)^2}\) different ways that you can arrange a sequence of \(2n\) bits where half are set and the other half are not.

Now let’s implement it. First, a factorial (!) function:

def fac(n):
    x = 1
    for i in range(1, n+1):
        x *= i
    return i

and now the actual formula:

def lattice_paths(n):
    return fac(2*n) / fac(n)**2

Inputting a value of n = 2 gives the answer to the 2x2 grid:

lattice_paths(2)
6

and inputting a value of n = 20 gives the answer to the question:

lattice_paths(20)
137846528820

There are 137846528820 unique lattice paths for a 20x20 grid!

More about combinatorics

As mentioned, this problem is a specific case of a more general problem in combinatorics. The general problem asks: “How many different unordered subsets of \(k\) elements from a set of \(n\) elements exist?” This is usually notated as \({n\choose k}\), read as “\(n\) choose \(k\)” (from a set of \(n\) elements, choose \(k\) of them). The formula for this is as follows:

\[{n\choose k} = \frac{n!}{k!(n-k)!}\]

In our case, \(n\) is the length of the bit sequence (number of places where we can place a \(1\)) and \(k\) is the number of \(1\)’s in the sequence. If we plug these in:

\[{2n\choose n} = \frac{2n!}{n!(2n-n)!} = \frac{(2n)!}{(n!)(n!)} = \frac{(2n)!}{(n!)^2}\]

we get the formula we derived!