Google Foobar: Bringing a Gun to a Guard Fight
Google’s Foobar challenge is a series of programming problems that used to be used to recruit potential developers. This problem was my favourite of all of them, mainly because it has a creative solution and requires no prior knowledge of theorems or algorithms.
The problem is as follows:
Uh-oh - you’ve been cornered by one of Commander Lambdas elite guards! Fortunately, you grabbed a beam weapon from an abandoned guard post while you were running through the station, so you have a chance to fight your way out. But the beam weapon is potentially dangerous to you as well as to the elite guard: its beams reflect off walls, meaning you’ll have to be very careful where you shoot to avoid bouncing a shot toward yourself!
Luckily, the beams can only travel a certain maximum distance before becoming too weak to cause damage. You also know that if a beam hits a corner, it will bounce back in exactly the same direction. And of course, if the beam hits either you or the guard, it will stop immediately (albeit painfully).
Write a function solution(dimensions, your_position, guard_position, distance) that gives an array of 2 integers of the width and height of the room, an array of 2 integers of your x and y coordinates in the room, an array of 2 integers of the guard’s x and y coordinates in the room, and returns an integer of the number of distinct directions that you can fire to hit the elite guard, given the maximum distance that the beam can travel.
The room has integer dimensions
[1 < x_dim <= 1250, 1 < y_dim <= 1250]. You and the elite guard are both positioned on the integer lattice at different distinct positions(x, y)inside the room such that[0 < x < x_dim, 0 < y < y_dim]. Finally, the maximum distance that the beam can travel before becoming harmless will be given as an integer1 < distance <= 10000.
One example of the problem is visually described below. Suppose the room is 4 x 2, you are standing at (1, 1), and the guard is standing at (2, 1). Then:
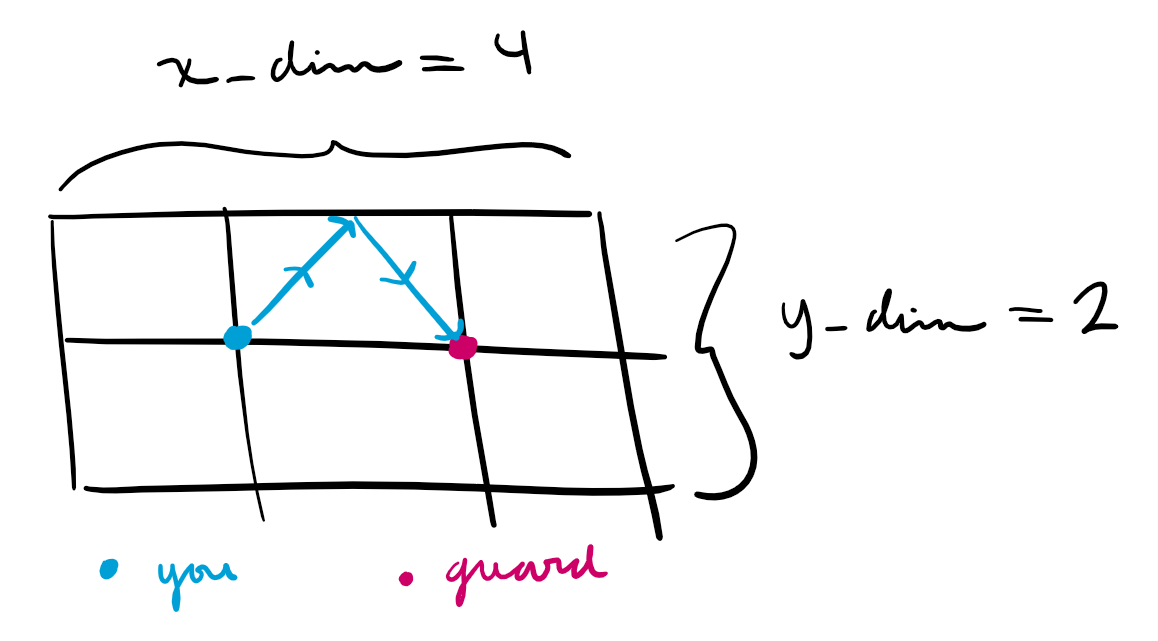
The blue dot represents your position and the red dot represents the guard’s position. The blue ray is a bullet shot that bounces off the top wall and hits the guard. You could also bounce off the bottom wall, or you could fire directly at the guard. The goal is to count how many different shots you could take that will hit the guard (without hitting you).
It’s tempting to want to write a simulation of the bullet ricocheting mechanics and directly count how many shots are valid. But, the key is realizing that a ray that reflects a wall at the same angle is equivalent to a ray that passes right through the wall into a mirror image of the room.
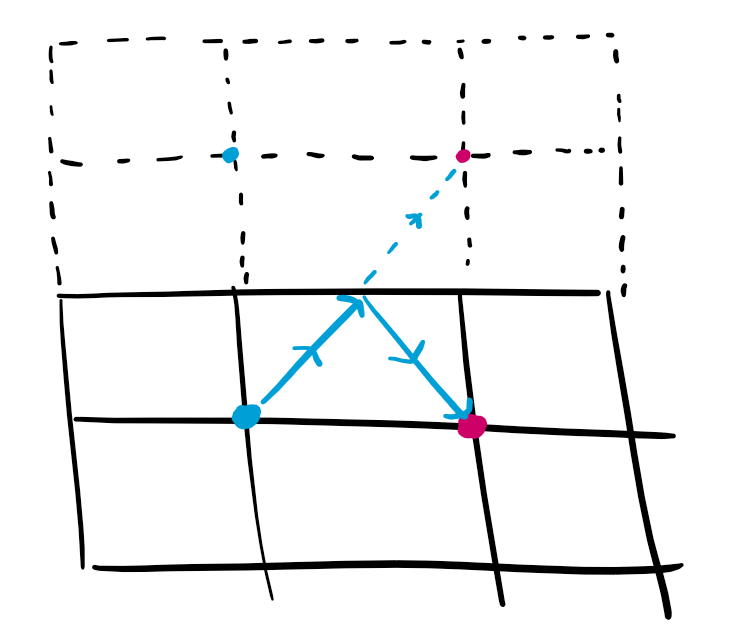
The benefit of this is that now every bullet has a straight-line path, making it easy to determine its length and whether or not it hits a guard. With this, an outline for the solution is possible.
- Generate all mirror images of the room in all directions that fit within the maximum range of the bullet.
- Remove any targets that are farther than the maximum range of the bullet.
- Compute the angle for every bullet path that hits a target and every bullet path that hits a guard.
- Count the number of bullet paths that hit a guard without hitting a player.
Generating mirror images
It’s enough to compute the upper and right mirror images (1st quadrant), since the other images are just reflections of the first quadrant. First, determine the maximum number of images to the right (x_imgs) and above (y_imgs) that can fit within the maximum bullet range (dist). Integer division is used here to prevent splitting a room in half. If even a little a bit of the reflected room is in range, the entire reflection will be included so as to not miss any guards. The guards inside the room outside of the maximal range can be filtered later.
x_imgs = (dist // dimensions[0]) + 2
y_imgs = (dist // dimensions[1]) + 2
Then, create x_imgs $\times$ y_imgs mirror images of the room in the first quadrant. Note that if the number of the image is even, it is an exact copy of the original room (it is a reflection of a reflection), but if its odd, the room needs to be reflected. The coordinates of each reflected guard and each reflected player are stored in respective your_pts and guard_pts lists.
ypx, ypy = your_pos[0], your_pos[1]
gpx, gpy = guard_pos[0], guard_pos[1]
your_pts = []
guard_pts = []
for y_img in range(y_imgs):
y_off = y_img * dimensions[1]
your_y = y_off + (ypy if not y_img % 2 else dimensions[1] - ypy) # even images are exact copies, odd needs to be reflected
guard_y = y_off + (gpy if not y_img % 2 else dimensions[1] - gpy) # even images are exact copies, odd needs to be reflected
for x_img in range(x_imgs):
x_off = x_img * dimensions[0]
your_x = x_off + (ypx if not x_img % 2 else dimensions[0] - ypx) # even images are exact copies, odd needs to be reflected
guard_x = x_off + (gpx if not x_img % 2 else dimensions[0] - gpx) # even images are exact copies, odd needs to be reflected
your_pts.append( (your_x, your_y) )
guard_pts.append( (guard_x, guard_y) )
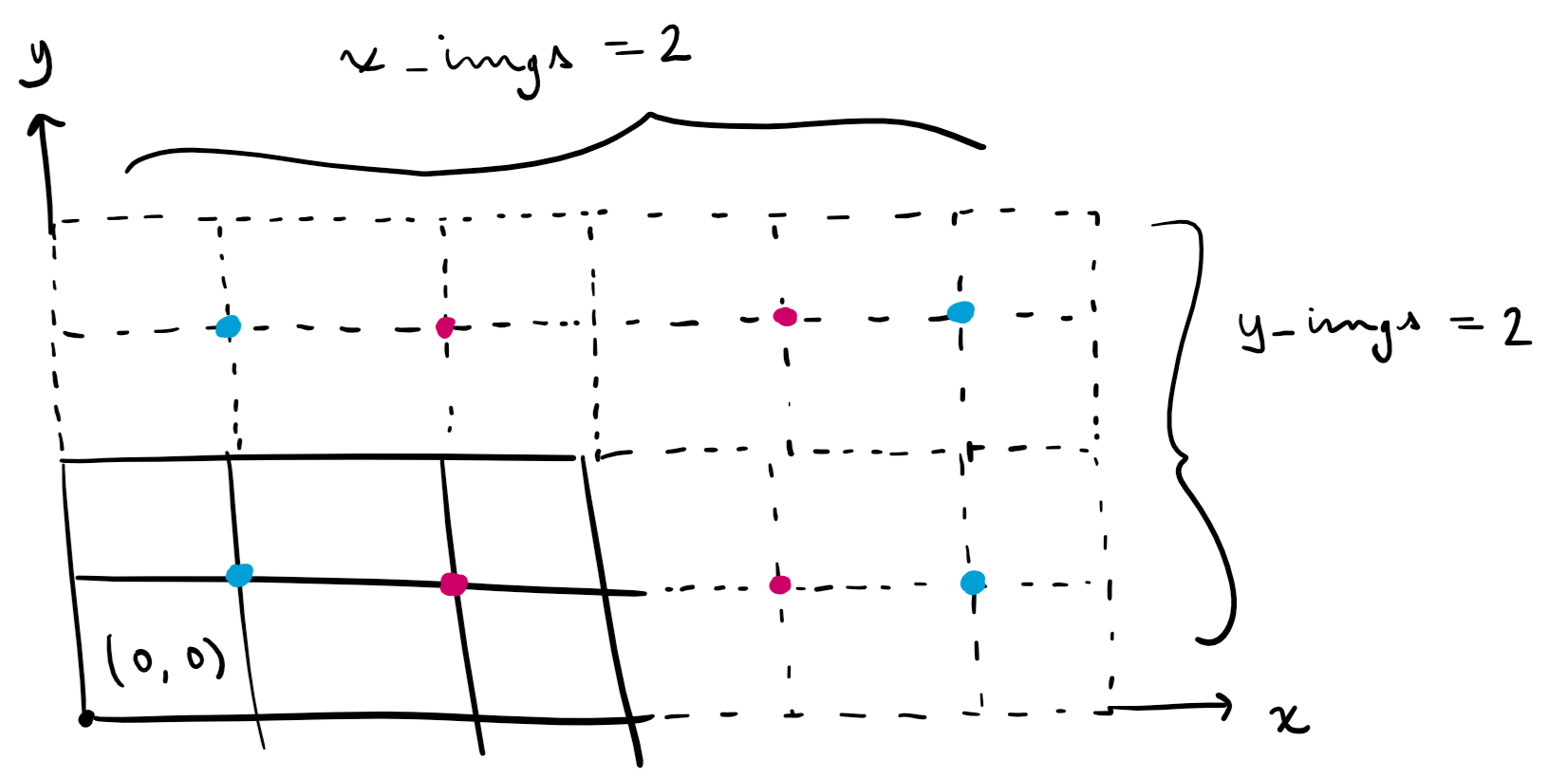
Now, image reflections in quadrants II, III, and IV can be included by reflecting the points in the first quadrant accordingly.
def include_reflections(pts):
'''Returns a list of reflected points in quadrants 1-4 from a list of 1st quadrant points'''
return [(xr, yr) for x, y in pts for xr, yr in ((x, y), (-x, y), (-x, -y), (x, -y))]
# ...
# include 2nd, 3rd, 4th quadrant pts from reflection of 1st quadrant pts
your_pts = include_reflections(your_pts)
guard_pts = include_reflections(guard_pts)
Removing targets outside of range
Since every bullet has a straight-line path, the length of the path is just the Euclidean distance $\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}$ between the player $(x_0, y_0)$ and the target $(x_1, y_1)$. To filter targets outside of range, remove any targets whose path is larger than the maximum range.
def distance(x0, y0, x1, y1):
'''Returns the distance between 2 points (x0, y0) and (x1, y1)'''
return ((x1-x0)**2 + (y1-y0)**2) ** 0.5
def filter_pts(x, y, pts, dist):
'''Removes points from pts that are farther than dist away from (x,y)'''
return [pt for pt in pts if distance(x, y, pt[0], pt[1]) <= dist]
# ...
# remove pts farther than the bullet distance away from the player
your_pts = filter_pts(ypx, ypy, your_pts, dist)
guard_pts = filter_pts(ypx, ypy, guard_pts, dist)
Computing bullet angles
There are now two list of coordinates: one representing all the guard reflections in range and a one representing all the player reflections in range. Each shot that hits a guard can then be represented by the angle the path forms with 0 degrees.
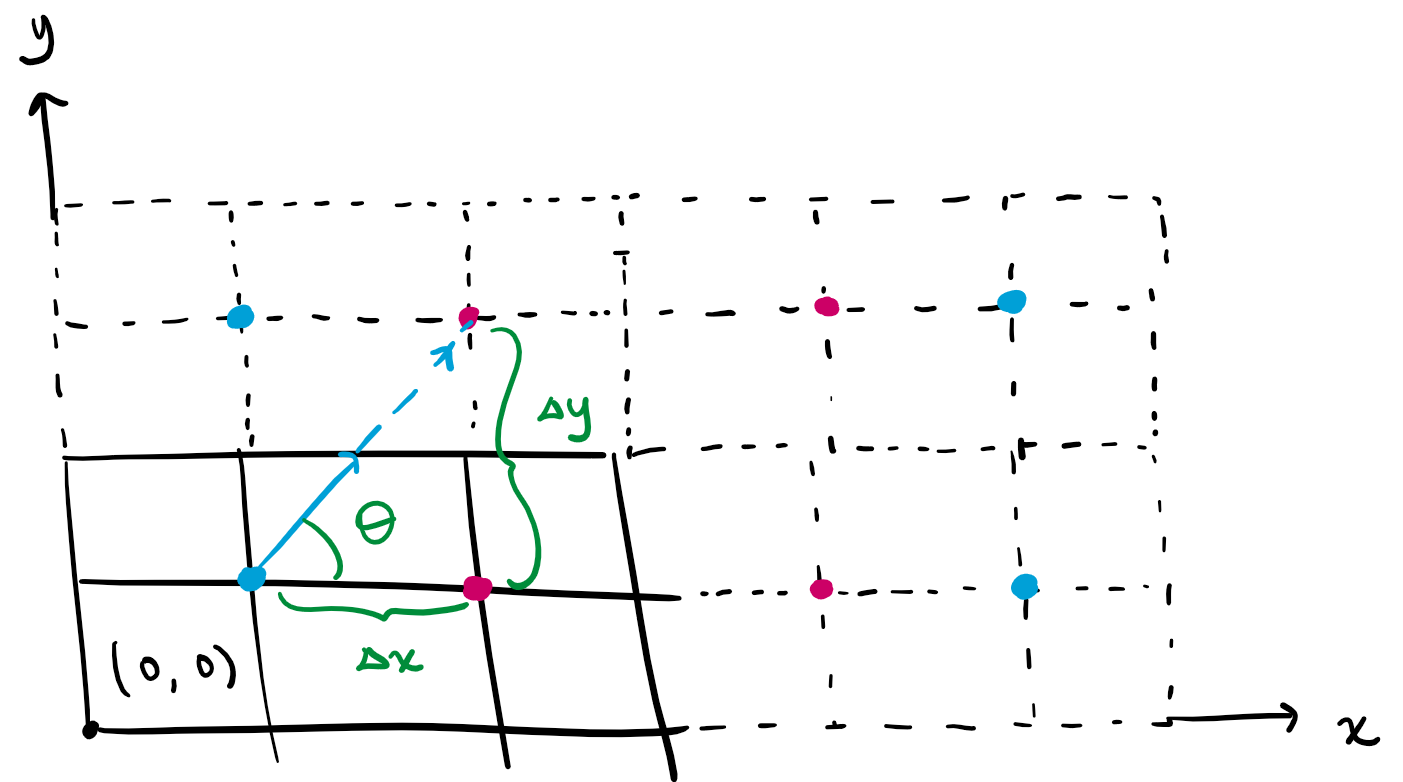
As shown, if the player’s position is $(x_0, y_0)$ and the target is $(x_1, y_1)$, then the corresponding angle can be calculated with $\theta = arctan(\frac{\Delta y}{\Delta x})$. The angle corresponding to each guard and to each player will be saved in a map guard_angles and player_angles respectively, which map angles to the corresponding target coordinates. If an angle corresponds to multiple guards, only the closest guard will be recorded; likewise for the closest player.
def angle(x0, y0, x1, y1):
# atan2 ensures the quadrant is correct and that theta = (-pi, pi)
return math.atan2(y1 - y0, x1 - x0) * (180/math.pi)
def get_angles(x0, y0, pts):
angles = {}
for x1, y1 in pts:
ang = angle(x0, y0, x1, y1)
if ang not in angles:
# the angle is unique
angles[ang] = (x1, y1)
else:
# the angle is not unique: only record the angle of the closest target along this path
recorded = angles[ang]
angles[ang] = min((x1, y1), recorded, key=lambda pt: distance(x0, y0, *pt))
return angles
# ...
# get map of (angle: pt) where pt is the closest point for a given angle
your_angles = get_angles(ypx, ypy, your_pts[1:])
guard_angles = get_angles(ypx, ypy, guard_pts)
Counting valid shots
Finally, only the shots that hit guards but miss players are considered. If the angle for a guard shot does not appear in your_angles, the shot certainly is not aligned with a player reflection. However, if it does appear in your_angles, the shot can only be counted if the guard is closer than the player (otherwise the player will be hit first!).
# count how many guards can be shot
shots = 0
for ang, pt in guard_angles.iteritems():
# a guard can only be shot if it's not aligned with a player reflection OR
# it is closer than an aligned player reflection
if ang not in your_angles or distance(ypx, ypy, *pt) < distance(ypx, ypy, *your_angles[ang]):
shots += 1
return shots
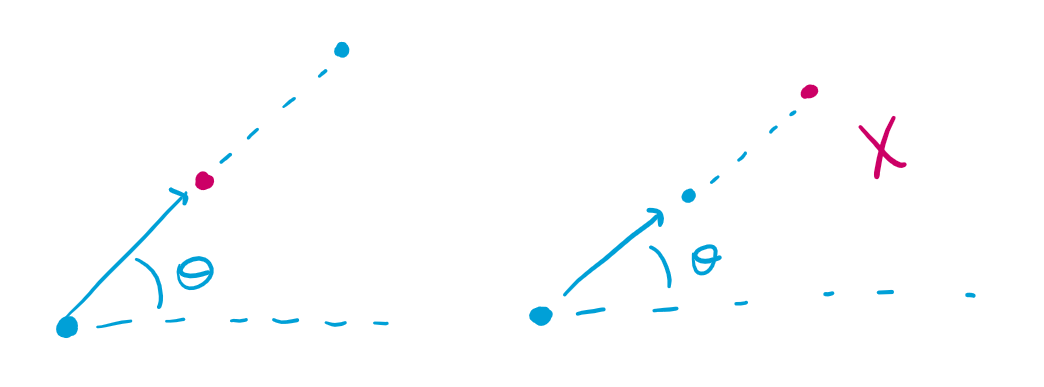
An example test case
For a $3 \times 2$ room where the player is positioned at $(1, 1)$ and the guard is positioned at $(2, 1)$ with a max bullet range of 4:
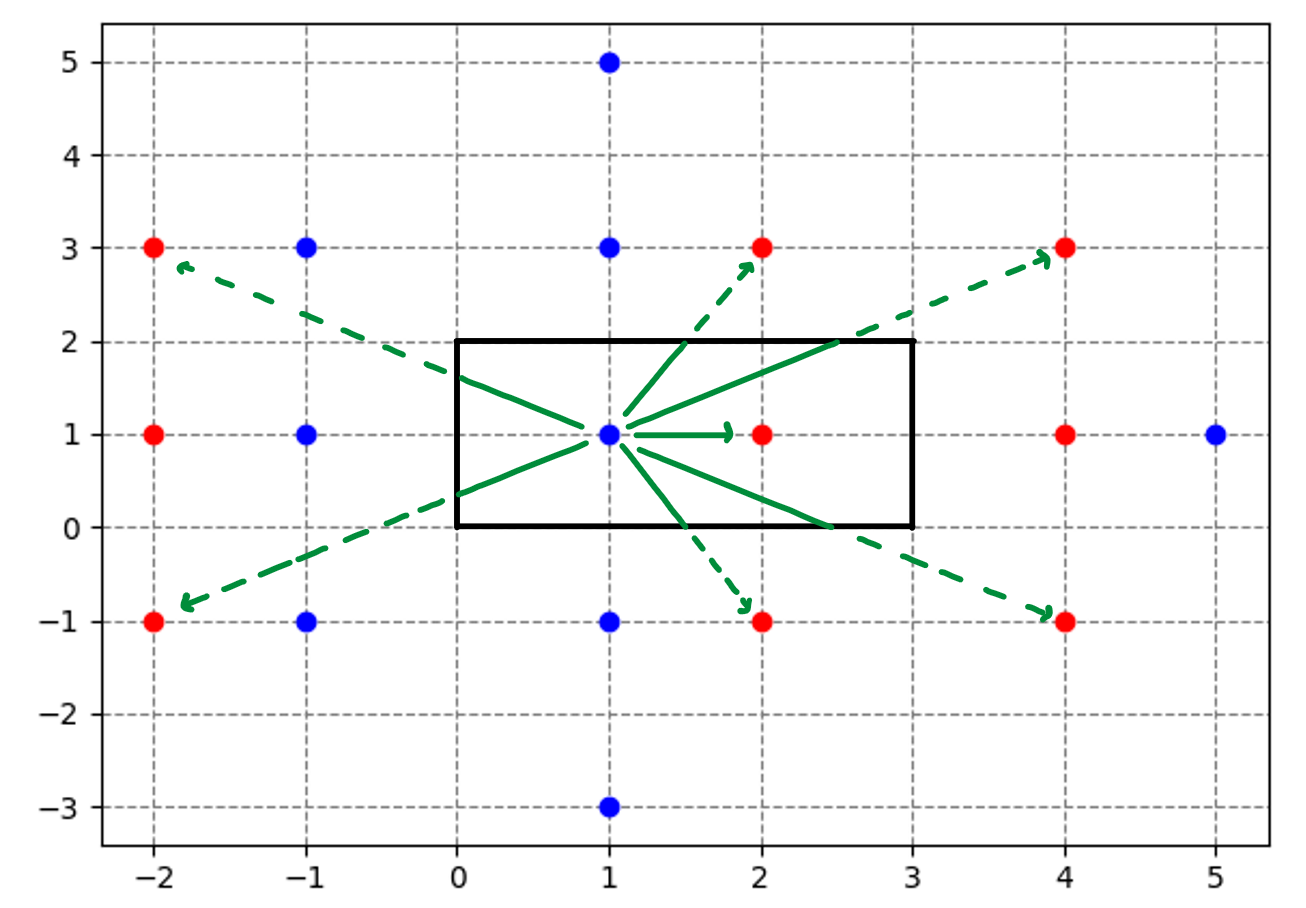
The black box represents the original room. The blue points are the player and their reflections and the red points are the guard and its reflections. The green paths are all valid bullet paths. Since their are 7 paths, the function returns 7.
def solution(dimensions, your_pos, guard_pos, dist):
ypx, ypy = your_pos[0], your_pos[1]
gpx, gpy = guard_pos[0], guard_pos[1]
# max number of lattice image copies that fit within dist
x_imgs = (dist // dimensions[0]) + 2
y_imgs = (dist // dimensions[1]) + 2
# find points of the first quadrant
your_pts = []
guard_pts = []
for y_img in range(y_imgs):
y_off = y_img * dimensions[1]
your_y = y_off + (ypy if not y_img % 2 else dimensions[1] - ypy)
guard_y = y_off + (gpy if not y_img % 2 else dimensions[1] - gpy)
for x_img in range(x_imgs):
x_off = x_img * dimensions[0]
your_x = x_off + (ypx if not x_img % 2 else dimensions[0] - ypx)
guard_x = x_off + (gpx if not x_img % 2 else dimensions[0] - gpx)
your_pts.append( (your_x, your_y) )
guard_pts.append( (guard_x, guard_y) )
# include 2nd, 3rd, 4th quadrant pts from reflection of 1st quadrant pts
your_pts = include_reflections(your_pts)
guard_pts = include_reflections(guard_pts)
# remove pts farther than the bullet distance away from the player
your_pts = filter_pts(ypx, ypy, your_pts, dist)
guard_pts = filter_pts(ypx, ypy, guard_pts, dist)
# get map of (angle: pt) where pt is the closest point for a given angle
your_angles = get_angles(ypx, ypy, your_pts[1:])
guard_angles = get_angles(ypx, ypy, guard_pts)
# count how many guards can be shot
shots = 0
for ang, pt in guard_angles.iteritems():
# a guard can only be shot if it's not aligned with a player reflection OR
# it is closer than an aligned player reflection
if ang not in your_angles or distance(ypx, ypy, *pt) < distance(ypx, ypy, *your_angles[ang]):
shots += 1
return shots
>>> solution([3,2], [1,1], [2,1], 4)
7
The full program can be found here.